Friday 22 May, 2015, 07:48 - Spectrum Management
Posted by Administrator
You may remember in this very month of last year, that Wireless waffle reported that various studies concerning the demand for radio spectrum for mobile services were replete with rather significant and obvious mathematical errors. It seems that these types of error which serve to highlight the poor plight of the mobile operators and their search for new spectrum may be systematic. This time it is the turn of Frontier Economics and their studies 'Economic assessment of C-band reallocation in the Arab States region' and 'Economic assessment of C-band reallocation in Africa'.Posted by Administrator
In them, they try and calculate the price of spectrum in a number of countries by considering the differences between the population density, average revenue per user (ARPU) and 3G penetration with a benchmark value derived from the price paid at auction in other countries. So where have they gone wrong?
 Imagine you are trying to calculate the overall appetite for bread to some ducks in a pond. The data you have tells you the density of ducks in the pond, the preference of the ducks for bread, and the area of the pond. Clearly:
Imagine you are trying to calculate the overall appetite for bread to some ducks in a pond. The data you have tells you the density of ducks in the pond, the preference of the ducks for bread, and the area of the pond. Clearly:- if the density of ducks increases, the appetite for bread will increase in direct proportion (that is to say that if the density of ducks doubles, then the appetite for bread will double);
- if the preference of the ducks for bread increases, similarly the appetite will increase in direct proportion, and
- if the area of the pond increases, the appetite for bread will increase, and again it will be directly proportional.
So it may come as a surprise, that in their studies, Frontier Economics consider a similar set of factors but instead of multiplying them together, they average them as page 16 of their report on Africa demonstrates:
We first calculate the country's population density, 3G penetration rate and ARPU as a percentage of the auction sample's average population density, 3G penetration rate and ARPU respectively. We then take a simple average of these three proportions to obtain the final adjustment factor.
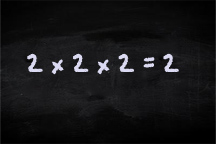 So if the ducks have the same preference for bread as the benchmark (e.g. the 'auction sample') and are just as densely packed, but the size of the pond is zero, the overall appetite should, of course, be zero. But if these factors are averaged, the result will not be zero. The average of 100%, 100% and 0% is... oh, come on now, the maths is pretty easy... 66%. Therefore, according to the economists at Frontier, the appetite for bread by NO ducks, is two-thirds of the benchmark value. And if the density, preference and area of the pond double and thus (as shown above) the appetite should increase by 800%, Frontier would no doubt claim that it only increases by a factor of 200% (the average of 200%, 200% and 200%, as it goes).
So if the ducks have the same preference for bread as the benchmark (e.g. the 'auction sample') and are just as densely packed, but the size of the pond is zero, the overall appetite should, of course, be zero. But if these factors are averaged, the result will not be zero. The average of 100%, 100% and 0% is... oh, come on now, the maths is pretty easy... 66%. Therefore, according to the economists at Frontier, the appetite for bread by NO ducks, is two-thirds of the benchmark value. And if the density, preference and area of the pond double and thus (as shown above) the appetite should increase by 800%, Frontier would no doubt claim that it only increases by a factor of 200% (the average of 200%, 200% and 200%, as it goes).Of course there is an argument to say that the factors that the report is trying to apply are not mutually exclusive so that multiplying them is not the right approach. But whatever the right approach is, taking the average is unlikely to be one of them.
 Maybe Frontier Economics flunked the statistics module in their maths exams. This would tend to be hinted at by the slogan on their web-site:
Maybe Frontier Economics flunked the statistics module in their maths exams. This would tend to be hinted at by the slogan on their web-site:We hope you'll find us a little different
What they mean by 'little' and 'different' may, of course, be in themselves a little different from someone else's understanding. Alternatively, the fact that they were being paid to do the calculations by the GSMA meant that they did them in a way that was 'a little different'. In either case a little different would seems to mean 'a little wrong'. So how does their slogan read now?
Whatever the cause, it seems that the mobile industry is replete with regulators, consultants and industry bodies who have forgotten how to use a calculator properly. As for the GSMA who should surely have checked for such glaringly self-evident miscalculated averages before publishing the reports, perhaps grotesquely skewed mathematical analyses are to their taste?
add comment
( 316 views )
| permalink
| 



 ( 2.9 / 10318 )
( 2.9 / 10318 )




 ( 2.9 / 10318 )
( 2.9 / 10318 )